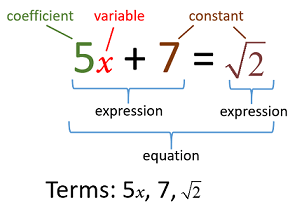
Intervals are ubiquitous in mathematical analysis. An interval can contain neither endpoint, either endpoint, or both endpoints.įor example, the set of real numbers consisting of 0, 1, and all numbers in between is an interval, denoted and called the unit interval the set of all positive real numbers is an interval, denoted (0, ∞) the set of all real numbers is an interval, denoted (−∞, ∞) and any single real number a is an interval, denoted. Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. In mathematics, a ( real) interval is the set of all real numbers lying between two fixed endpoints with no 'gaps'. All numbers greater than x and less than x + a fall within that open interval. For other uses, see Interval (disambiguation).

For intervals in order theory, see Interval (order theory). This article is about intervals of real numbers and some generalizations.